Blenderで描いたモデルをUnityで物理演算するときの慣性モーメントの話

　こんにちは．changです．

　物凄くニッチな内容ですが，Blenderで作ったモデルをUnityに移植して物理演算する際の慣性モーメントの与え方について解説します．この情報を必要とする方は世の中に殆どいらっしゃらないと思いますが，，，

1. 慣性モーメントとは？

　一言で言うと，回転運動版の質量です．運動方程式が

$ma = F$

だと言うのは，高校物理で教わりますね．細かい事を言うと，これは並進の運動の方程式です． $m$ は質量を， $a$ は加速度を， $F$ は外力をそれぞれ表しています．因みに，加速度 $a$ は位置の二階微分であり， $\ddot x$ とも書けます．

　ここで，運動方程式を回転版で表すと，

$I \ddot \theta = T$

になります． $I$ は慣性モーメント， $\ddot \theta$ は角加速度， $T$ はトルクを表します．並進の運動方程式と比較すると， $m$ → $I$ ， $a$ (= $\ddot x$ ) → $\ddot \theta$ ， $F$ → $T$ にそれぞれ対応しています．並進運動を解く際に物体の質量(わかりやすく言うと，重さ)が重要になるのは，何となく理解出来ます．それと同様に，回転の運動を正確に解く際には慣性モーメントが不可欠なのです．

　慣性モーメントの計算方法の詳細は省略します．話を簡単にする為に物体内の密度を一様と仮定すると，慣性モーメントは物体の形状のみで決まります．例えば直方体*1ならば:

直方体．重心を原点，x方向の長さをb，y方向の長さをb，z方向の長さをlとしています

$I_{x} = \frac{1}{12} m (a^2 + l^2)$

$I_{y} = \frac{1}{12} m (b^2 + l^2)$

$I_{z} = \frac{1}{12} m (a^2 + b^2)$

円柱ならば*2:

$I_{x} = \frac{1}{4} m (a^2 + \frac{1}{3} l^2)$

$I_{y} = \frac{1}{4} m (a^2 + \frac{1}{3} l^2)$

$I_{z} = \frac{1}{2} m a^2$

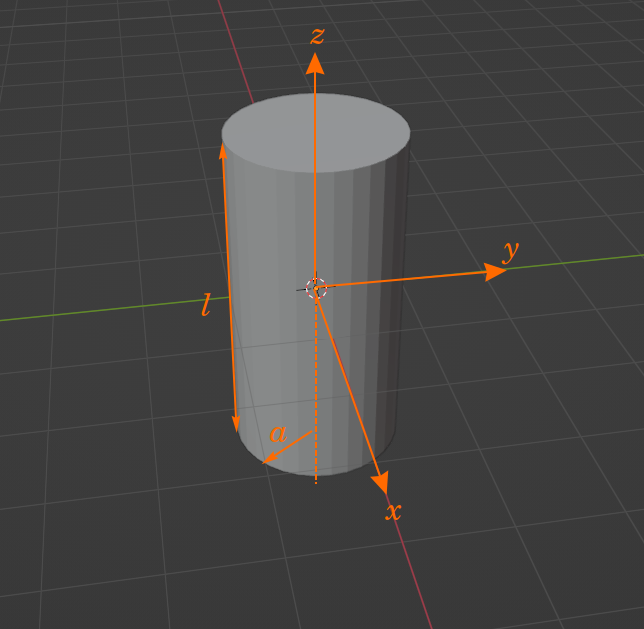
です．

Note:
直方体や円柱の様な基本図形の慣性モーメントは上記のような基本式で表現出来ますが，一般的には物体形状に応じた積分を数値的に解く必要があります． CADソフトの多くが，その機能を有しています．

2. Unityの慣性モーメント

2. 1 基本図形(凹無し)

　UnityでCubeやCylinderの物理演算をするとき，特に慣性モーメントを意識しなくても動いてしまいます．あれは，慣性モーメントが勝手に設定されているからです．試しに，Cubeで見てみます．

GameObjectからCubeを追加 → Y方向のスケールを2に変更 → rigidbodyを割り当て

　Inspectorを拡大します．

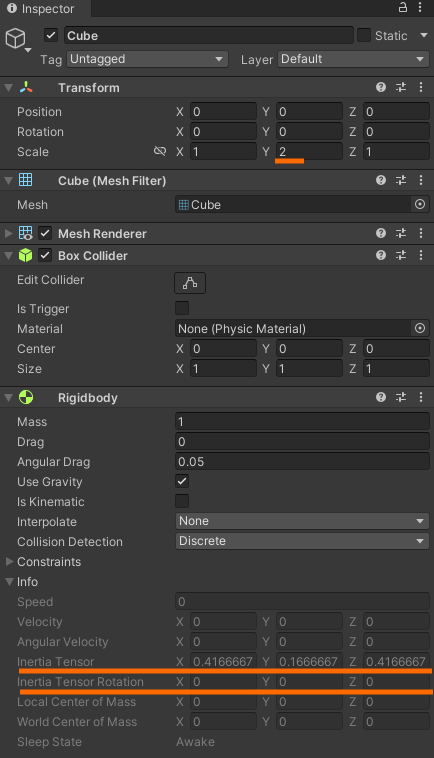
　Inertia Tensor， Inerita Tensor Rotationという部分に注目して下さい．これが慣性モーメントです．英語表記になっていてすみません．おそらく日本語表記では，慣性テンソル，慣性主軸かと思います．

　上述の直方体の基本式を使って慣性モーメントを求めてみます． $m = 1.0$ ， $a = 1.0$ ， $b= 1.0$ ， $l = 2.0$ ですので，

$I_{x} = 0.416...$

$I_{y} = 0.416...$

$I_{z} = 0.166...$

になります． UnityがY上なので解り難いですが，Unityが設定した慣性モーメントと一致しています．少し値を見てみると， $I_x = I_y$ になっています．これは，今描いている直方体の $x$ 方向と $y$ 方向の長さが等しいからです．また， $I_z$ だけ少し小さな値になっています．これは， $z$ 軸周りに回転し易いという事です．長手を振り回す $x$ 軸や $y$ 軸よりも，長手に沿って回す $z$ 軸周りの方が小さな力で回せそうなのは直感と一致します．

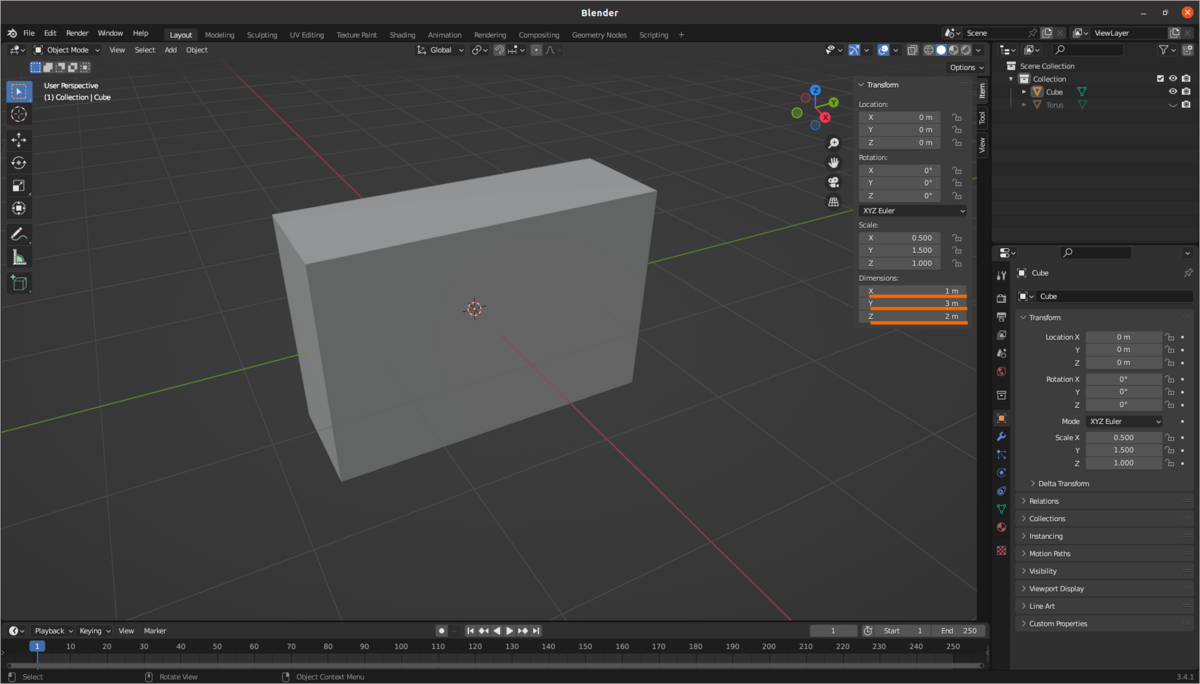
　 $I_x = I_y$ のままだとこの後の処理で計算が正しく行われたか判り難いので，Z方向のスケールを3に変えます．

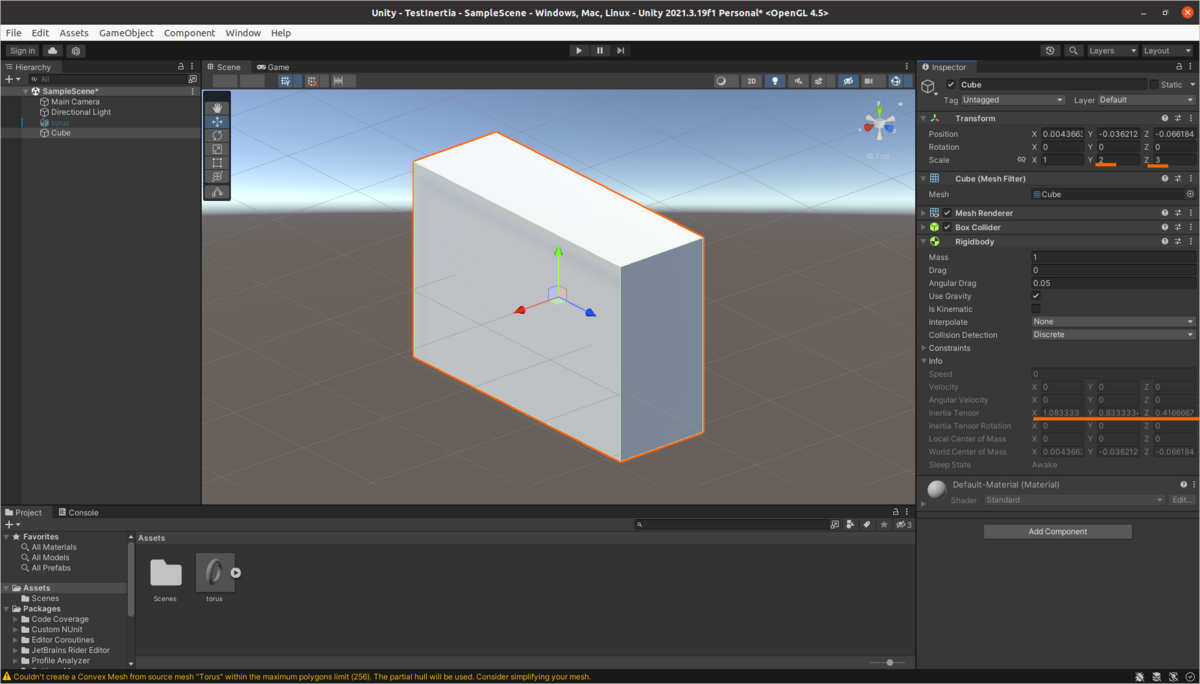
　Inertia Tensorは，X 1.083...，Y 0.833...，0.416...，になりました．この値も基本式と一致しています．

2. 2 複雑形状(凹有り)

　CubeやCylinderの様な単純形状の場合，慣性モーメントの設定はUnityにまかせて構いません．問題となるのは，複雑形状の場合です．

　例えば，BlenderでTorusを描いてみます．

　Unityに取り込む為にfbx形式でエキスポートします．

FBXエキスポート．ScaleをFBX All，ForwardをY，UpをZとします

　Unityに取り込みました．

エキスポートしたFBXファイルをUnityのAssetsにドラッグ&ドロップし，Hierarchyに追加します

　InspectorでTransformをみると，RotationのXが-90になっています．これはBlenderではZ上(左ネジ)の座標系をY上(右ネジ)のUnity座標系に変換している為です．

Note:
回転するだけでは右ネジのままなので，インポート時にX方向が反転されているかも知れません(要確認)．

　物理演算を行う為に，モデルにColliderとRigidbodyを割り当てます．例えばBoxColliderを選ぶとこんな感じになります．

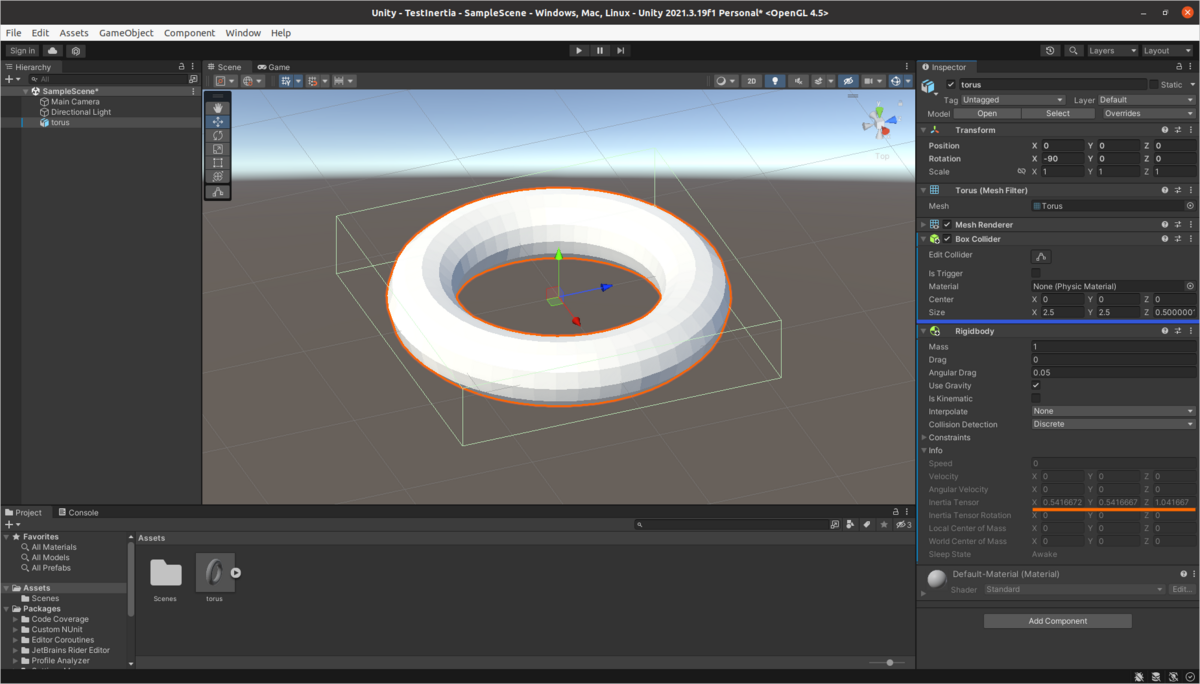
　緑の線で見えるのがColliderです．モデルを内包する最も小さな直方体になります． RigidbodyのInertia Tensorをみると，X 0.541...，Y 0.541...，Z 1.044...になっています．これは直方体の基本式にm = 1.0，x = 2.5，y = 2.5，z = 0.5と与えた場合に一致します．つまり，UnityはコライダーにBoxColliderを指定すると，慣性モーメントもBox(直方体)で計算する仕様になっています． 接触判定だけであればBoxで大雑把に行って問題無い場合も多そうですが，運動計算では大問題です．全く異なる形状の物体の運動を解く事になります．

　物理演算の精度を上げる方法として，(計算負荷が大きくなるので好まれませんが)MeshColliderがあります．

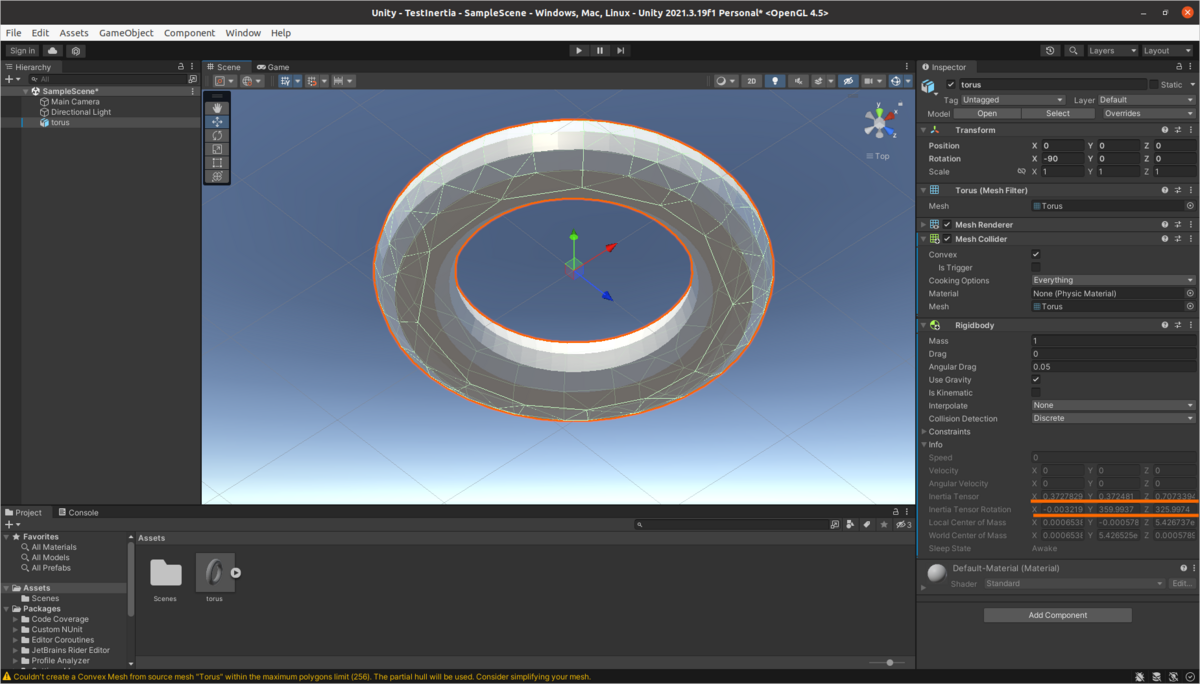
　緑の線がモデルの形状に沿う様になり，Inertia Tensorの値も何だか変わりました． BoxColliderを使うよりはマシですが，実は，Torusの穴は無視されています(=穴の無いドーナツ状態)．これもUnityの仕様として，MeshColliderでConvex(凹無し)を指定しないと接触判定が出来ないからです．当たり判定を安定させる為の仕組みなのでしょう．

　偉そうな物言いになって恐縮ですが，ここまではある程度一般的というか，多くの方が理解されていると思います．この記事の本題はこの先です．今，慣性モーメントも穴無し(凹無し)で計算されているという点です．

　自身の体重と照らし合わせるとイメージしやすいですが，軽量化すると駆動系への負荷が減って機敏に動ける様になります．これは，慣性モーメントが減るからです．多くの工業製品が軽量化の為の穴抜きを採用しているのも，同じ理由です． 物体運動に対してそれ程までに影響の大きい慣性モーメントの値を，Unityは当たり判定の軽さを優先して犠牲にしているのです．これは，凄く残念な感じがします．

Note:
当たり判定を凹で考慮する裏技(?)も一応あるのですが，今回は割愛します．

3. numpy-stlを使った慣性モーメント計算

3.1 慣性テンソル

　CADソフトウェアの多くが，慣性モーメントの計算機能を持っています．例えば，この記事*3 *4ではAutodeskのFusion 360を使っています．大変素晴らしい記事で参考にさせて頂いたのですが，私は学生ではないので無償版のFusion 360を使えません． FreeCAD等の無償素材を色々試した結果，numpy-stlに落ち着きました．

　先程使った直方体と同じ図形をBlenderで描きます．

BlenderでCubeを追加．DimensionをX 1.0，Y 3.0，Z 2.0に指定．Scaleではなく，Dimensionを指定する

　numpy-stlで読み込む為に，stl形式でエキスポートします．

　numpy-stlでstlモデルを読み込んで慣性モーメントを計算します．

from stl import mesh

stl_data = mesh.Mesh.from_file("./cube.stl")
volume, cog, inertia = stl_data.get_mass_properties()
print("volume")
print(volume)
print("center of mass")
print(cog)
print("inertia")
print(inertia/volume)

　こんな感じで出力されます．

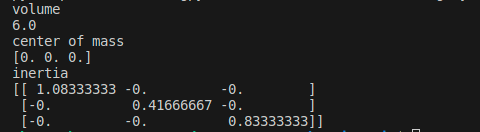
　慣性モーメントは，3×3の行列形式(=テンソル)で出力されます．以降で触れる内容になりますが，今は慣性主軸とXYZ軸が一致しているので，対角行列でかつ対角成分にXYZ軸周りの慣性モーメントが配置されています．座標系の関係でYとZが反転している事以外は，Unityでの計算結果と一致していますね．この値をUnity側で指定できれば良さそうです．

Note:
上記のソースでinerita/volumeとしているのは，numpy-stlが密度1 kg / m³で動く為です(そのままだと，質量 6 kgで計算される)． Unity側ではmass = 1.0としていたので，質量を合わせる為に正規化しています．

3.2 慣性主軸

　一番苦労したところです．これまで議論して来ませんでしたが，UnityのRigidbodyにはInertia Tensorとは別にInertia Tensor Rotationという項目があります．日本語で言うと慣性主軸です．慣性主軸というのは，慣性モーメントの主成分分析です．つまり，Unityは，モデルの形状を表現している座標系に沿ってではなく，モデルが最も回転し易い軸構成に沿って慣性モーメントを表記する仕様になっています．これまで描いていた直方体では慣性主軸がたまたまX軸やY軸に一致していた為に，Inertia Tensor Rotationが全て0だったのです．

　試しに，先刻Blenderで描いた直方体をX軸周りに30度回転してみます．

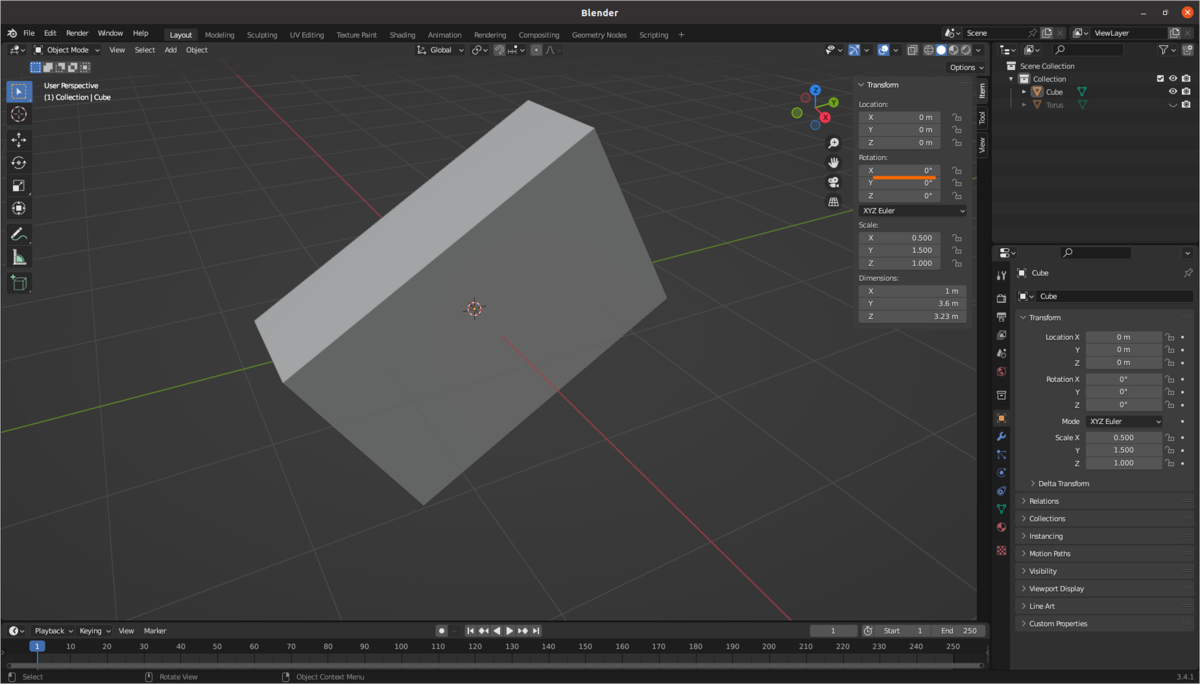
Blender側でCubeをX軸周りに30度回転．RotationをApplyした後のキャプチャなので，Rotationは全て0になっている

　この状態でFBXエキスポートし，Unity側で慣性モーメントを計算させてみます．

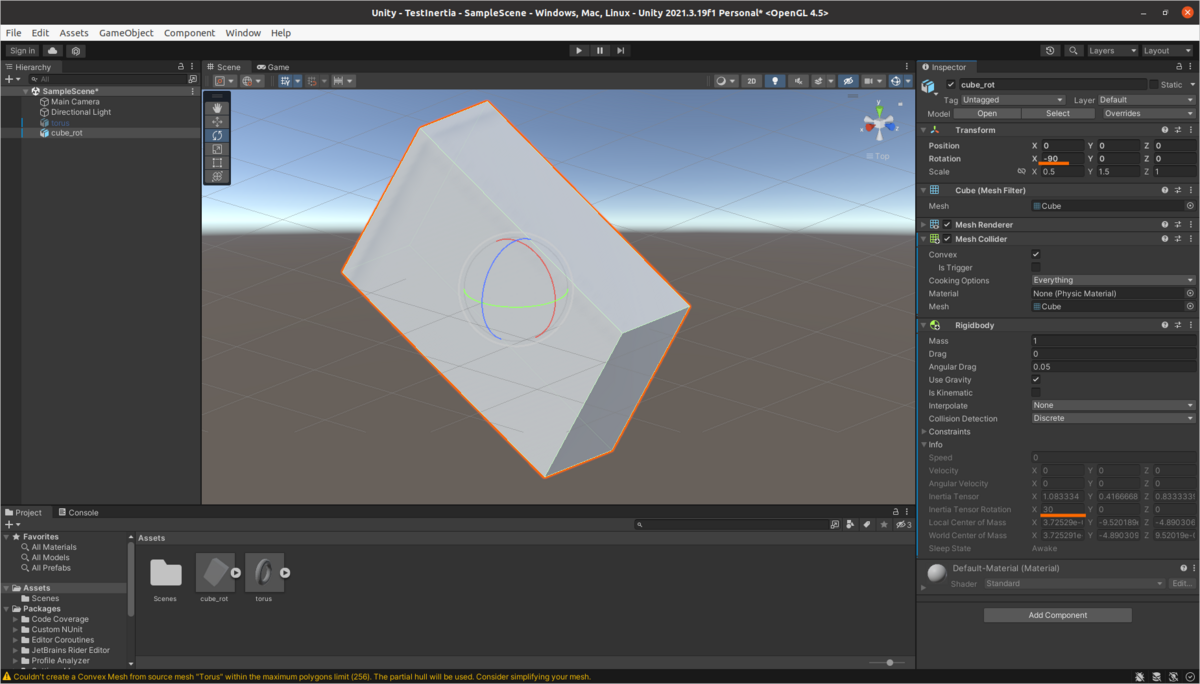
Unity側で慣性モーメントを計算させた結果．Inertia Tensor RotationのXが30になっている

　Inertia Tensorの値はそのままで，Inertia Tensor RotationのXが30になりました．図形を30度回転させた事を反映しています．また，2. 1 でUnityで同じ図形を描いたときのInertia Tensorと比較すると，YとZが反転しています．これは先程から再三観られる様に，UnityはY上，BlenderはZ上という座標系の相違によるものです．この相違は，TransformのRotation X -90で吸収されています．

　ポイントが2つあります．(1) BlenderでObject→Apply→Rotationを行ってからFBXエキスポートする事と，(2) Unity側はBoxColliderではなくてMeshColliderを使う事です．(1)をしないと，図形の回転がInertia Tensor RotationではなくTransformのRotationに反映されます．(2)をBoxColliderにしてしまうと，元図形を無視してXYZ軸に沿った大きな直方体コライダーが出来ます．

　では，numpy-stlで求めた慣性テンソルをUnity式，つまり慣性主軸に沿った慣性テンソルと慣性主軸に変換していきます．慣性テンソルを固有値解析すれば良さそうです．回転を与えた直方体をBlenderからstlエキスポートし，先刻と同様にnumpy-stlで慣性テンソルを求めます．

import numpy as np
from stl import mesh

stl_data = mesh.Mesh.from_file("./cube_rot.stl")
volume, cog, inertia = stl_data.get_mass_properties()
print("volume")
print(volume)
print("center of mass")
print(cog)
print("inertia tensor")
print(inertia/volume)

print("### eigen value analysis ###")

eig, vec = np.linalg.eig(inertia/volume)
print("eigen value")
print(eig)
print("eigen vector")
print(vec)

　こんな出力になります．

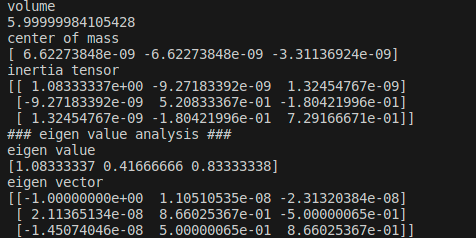
　少し見難いので必要な結果を書き出します． numpy-stlの慣性テンソルは図形を回転させた前後で以下の様に変化しました．

回転前:

$\begin{bmatrix} 1.803 & 0.0 & 0.0 \\ 0.0 & 0.416 & 0.0 \\ 0.0 & 0.0 & 0.833 \\ \end{bmatrix}$

回転後:

$\begin{bmatrix} 1.803 & 0.0 & 0.0 \\ 0.0 & 0.5208 & -0.1804 \\ 0.0 & -0.1804 & 0.7291 \\ \end{bmatrix}$

　対角行列ではなくなったのは，慣性主軸がY軸とZ軸に一致しなくなったためです．続けて固有値解析の結果をみてみます．

固有値:

$\begin{bmatrix} 1.803 & 0.416 & 0.833 \\ \end{bmatrix}$

固有ベクトル:

$\begin{bmatrix} 1.0 & 0.0 & 0.0 \\ 0.0 & 0.866 & -0.5 \\ 0.0 & 0.5 & 0.866 \\ \end{bmatrix}$

　固有値分析する事によって，慣性テンソルを回転を与える前の(慣性主軸がXYZ軸に一致していた)慣性モーメント：固有値と，慣性主軸：固有ベクトルに分離することが出来ました． sin(30度) = 0.5，cos(30度) = 0.866ですので，固有ベクトルはx軸周りに30度回転する回転行列になっている事が判ります．求めた固有値をInertia Tensorに，固有ベクトルをInertia Tensor Rotationに与えていきます．

3. 3 Unity座標系との整合

　実はもう一工夫要ります．

　numpy-stlで求めた固有値と固有ベクトルが本当にUnityのInertia TensorとInertia Tensor Rotationと一致しているか確かめてみます．先程，Blenderから移植した直方体に下記のC# Scriptをアタッチし，Unityが内部的に保持している慣性主軸をコンソールに出力します．

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class cube_rot : MonoBehaviour
{
    Rigidbody rb;
    // Start is called before the first frame update
    void Start()
    {
        rb = GetComponent<Rigidbody>();
        Matrix4x4 matrix = Matrix4x4.identity;
        matrix.SetTRS(Vector3.zero, rb.inertiaTensorRotation, Vector3.one);
        Debug.Log("RationMatix");
        Debug.Log(string.Format("{0:F3}, {1:F3}, {2:F3}", matrix.m00, matrix.m01, matrix.m02));
        Debug.Log(string.Format("{0:F3}, {1:F3}, {2:F3}", matrix.m10, matrix.m11, matrix.m12));
        Debug.Log(string.Format("{0:F3}, {1:F3}, {2:F3}", matrix.m20, matrix.m21, matrix.m22));
        Debug.Log("EulerAngles");
        Debug.Log(matrix.rotation.eulerAngles);
    }
}

　Inspectorでは何故かEuler角で表示されますが，Inertia Tensor Rotationの実体はQuaternionです．それを回転行列に変換してログ出力しています．省略してしまいますが，このケースではnumpy-stlから固有ベクトルとUnity内部の慣性主軸が一致しました．

　次に，X軸周りに30度回転させた直方体を，更にY軸周りに-15度，Z軸周りに225度回転させます．

Blender側でCubeをX軸周りに30度，Y軸周りに-15度，Z軸周りに225度回転．RotationをApplyした後のキャプチャなので，Rotationは全て0になっている

　numpy-stlで固有値解析をしていみると，こんな結果になりました．

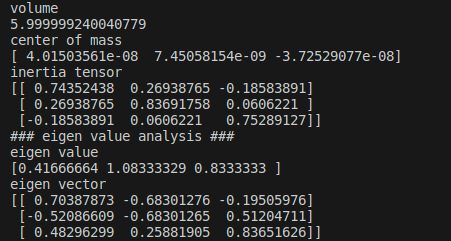
　見難いのでまた結果を書き出します．

固有値:

$\begin{bmatrix} 0.416 & 1.803 & 0.833 \\ \end{bmatrix}$

固有ベクトル:

$\begin{bmatrix} 0.7038 & -0.6830 & -0.1950 \\ -0.5208 & -0.6830 & 0.5120 \\ 0.4829 & 0.2588 & 0.8356 \\ \end{bmatrix}$

　一方，Unity側はこうなりました．

固有値
=Inertia Tensor:

$\begin{bmatrix} 0.416 & 1.803 & 0.833 \\ \end{bmatrix}$

固有ベクトル
=Inertia Tensor Rotation:

$\begin{bmatrix} 0.7038 & -0.6830 & 0.1950 \\ 0.5208 & 0.6830 & 0.5120 \\ -0.4829 & -0.2588 & 0.8356 \\ \end{bmatrix}$

　偶然ですが，固有値の順番は一致しています．ですので，固有ベクトルも一致して欲しいのですが，，，そうなりません．もう少し考察が要りそうです．

　良く観ると，numpy-stlの固有ベクトルが右手系になっていません．これは，np.linalg.eigが出してくる固有値の方向がランダムになるからです．

Note:
固有ベクトルの順番もバラバラになります．今回はたまたま順番がUnity側と一致しましたが，一致しない場合は固有値の順番に併せて固有ベクトルを並べ直す必要があります．

　という訳で，3列目を1列目と2列目の外積で再定義します．

numpy-stlの固有ベクトル:

$\begin{bmatrix} 0.7038 & -0.6830 & 0.1950 \\ -0.5208 & -0.6830 & -0.5120 \\ 0.4829 & 0.2588 & -0.8356 \\ \end{bmatrix}$

　改めてUnity側の固有ベクトル(Inertia Tensor Rotation)と比較すると，2行目と3行目の符号を入れ替えると一致する事がわかります．これは何故だか分かりません．幾つかのケースを試しましたが，必ずこうなりました(X軸30度回転の直方体で符号の反転が必要ないのは，Y軸とZ軸に対してシンメトリーな図形だからです)．おそらく，Unity座標系でY上になる際にX軸が反転する事に起因していると思います．

　少々経験的な部分もあるのですが，以上をまとめると：
(1) numpy-stlで慣性テンソルを求める
(2) (1)をnp.linalg.eigで固有値分解する
(3) (2)で求めた固有値をUnityのinertiaTensorに与える
(2) (2)で求めた固有ベクトルの2行目と3行目の符号を反転し，InertiaTensorRotationに与える

4. Unityへの値の与え方

　InspectorのInertia TensorとInertia Tensor RotationはUIから触れません． C#スクリプトから指定する必要があります．疲れてしまったので省略しますが，固有値をRigidbody.inertiaTensorに，固有ベクトルをRigidbody.inertiaTensorRotationに代入します． Rigidbody.inertiaTensorRotationはQuaternionで表現されてますので，固有ベクトルをQuaternionに変換する必要があります．

5. むすび

　長文になりました．参考になる情報が少なく，結構大変でした．

　冒頭にも書いた通りニッチな内容の記事でしたが，こんな風に世の中の方があまり触れないと言うか，難しすぎて毛嫌いするような事を書いてこそ面白いです．弄れ物の自分の存在価値を感じると言うか... 去年は技術系の記事を殆ど書けなかったので，今年はもう少し頑張りたいです．

*1:https://domeblog.net/momentofinertia_rectangular/

*2:https://moment-of-inertia.jp/moi/circular_cylinder.html

*3:https://mtkbirdman.com/unity-aerodynamiccalculator#toc3

*4:https://mtkbirdman.com/fusion360-property-inertia

オッサンはDesktopが好き

自作PCや機械学習、自転車のことを脈絡無く書きます